6 min read

Swings and Misses

2019/05/06

I going to work more with data from mlbgameday.

library(mlbgameday)
library(magrittr)
library(ggplot2)
library(dplyr)
## 
## Attaching package: 'dplyr'
## The following objects are masked from 'package:stats':
## 
##     filter, lag
## The following objects are masked from 'package:base':
## 
##     intersect, setdiff, setequal, union

Get data.

# Takes hours to get all the data for the year
dat <- get_payload(start = "2018-01-01", end = "2018-12-31")

Get pitcher names from at bat data.

d2 <- inner_join(dat$pitch, dat$atbat, by=c("num", "url"))

Pick out the swinging strikes.

d2 %>% filter(des %in% c("Swinging Strike", "Swinging Strike (Blocked)")) %>% group_by(pitcher_name) %>% summarize(N=n()) %>% arrange(desc(N))
## # A tibble: 878 x 2
##    pitcher_name         N
##    <chr>            <int>
##  1 <NA>             10872
##  2 Max Scherzer       656
##  3 Jacob deGrom       583
##  4 Justin Verlander   563
##  5 Gerrit Cole        544
##  6 Blake Snell        519
##  7 Patrick Corbin     506
##  8 Carlos Carrasco    504
##  9 Chris Sale         472
## 10 Trevor Bauer       461
## # ... with 868 more rows

These names are the ones we’d expect.

Who has the highest proportion of pitches as swinging strikes?

d2 %>% filter(!is.na(pitcher_name)) %>% group_by(pitcher_name) %>% summarize(N=n(), Nss = sum(des %in% c("Swinging Strike", "Swinging Strike (Blocked)"))) %>% mutate(pSS = Nss / N) %>% arrange(desc(pSS))
## # A tibble: 940 x 4
##    pitcher_name        N   Nss   pSS
##    <chr>           <int> <int> <dbl>
##  1 Brandon Brennan     8     6 0.75 
##  2 Ben Rowen          11     8 0.727
##  3 Brady Feigl         9     6 0.667
##  4 Joe Mantiply        9     6 0.667
##  5 Andrew Schwaab     15     9 0.6  
##  6 Nick Pasquale       5     3 0.6  
##  7 Domingo Tapia      12     7 0.583
##  8 Cesar Vargas       18     9 0.5  
##  9 Joe Gunkel          6     3 0.5  
## 10 Malcom Culver      44    22 0.5  
## # ... with 930 more rows

Unsurprisingly these are only guys with few pitches. Lets only pick out pitchers with at least 300 pitches.

d2 %>% filter(!is.na(pitcher_name)) %>% group_by(pitcher_name) %>% summarize(N=n(), Nss = sum(des %in% c("Swinging Strike", "Swinging Strike (Blocked)"))) %>% mutate(pSS = Nss / N) %>% arrange(desc(pSS)) %>% filter(N >= 300)
## # A tibble: 505 x 4
##    pitcher_name       N   Nss   pSS
##    <chr>          <int> <int> <dbl>
##  1 Josh Hader      1575   325 0.206
##  2 Hector Neris     853   176 0.206
##  3 Marcus Walden    317    65 0.205
##  4 Edwin Diaz      1266   245 0.194
##  5 Sean Doolittle   735   141 0.192
##  6 Dominic Leone    485    93 0.192
##  7 Ryan Pressly    1300   244 0.188
##  8 Jose Leclerc    1035   190 0.184
##  9 Joshua Lucas     316    57 0.180
## 10 Carson Smith     339    61 0.180
## # ... with 495 more rows

The pitchers best at missing bats are Josh Hader, Hector Neris, and Marcus Walden. Unsurprisingly these are all relievers.

If we set a higher bar for N, we can see the best starting pitchers.

d2 %>% filter(!is.na(pitcher_name)) %>% group_by(pitcher_name) %>% summarize(N=n(), Nss = sum(des %in% c("Swinging Strike", "Swinging Strike (Blocked)"))) %>% mutate(pSS = Nss / N) %>% arrange(desc(pSS)) %>% filter(N >= 2000)
## # A tibble: 116 x 4
##    pitcher_name        N   Nss   pSS
##    <chr>           <int> <int> <dbl>
##  1 Max Scherzer     3728   656 0.176
##  2 Blake Snell      3104   519 0.167
##  3 Jacob deGrom     3634   583 0.160
##  4 Chris Sale       2944   472 0.160
##  5 Patrick Corbin   3252   506 0.156
##  6 Carlos Carrasco  3249   504 0.155
##  7 Masahiro Tanaka  2811   429 0.153
##  8 Gerrit Cole      3651   544 0.149
##  9 Jack Flaherty    2730   406 0.149
## 10 James Paxton     2738   404 0.148
## # ... with 106 more rows

Let’s plot SS rate by pitcher and plot N vs Nss. This is a nasty plot. I put both axes on logs, used colors to show the best/worse pSS, and tried to add names.

d2 %>% filter(!is.na(pitcher_name)) %>% group_by(pitcher_name) %>% summarize(N=n(), Nss = sum(des %in% c("Swinging Strike", "Swinging Strike (Blocked)"))) %>% mutate(pSS = Nss / N) %>% arrange(desc(pSS)) %>% filter(Nss>0, N>1000) %>% 
  {(ggplot(., mapping=aes(N, Nss, color=pSS)) + geom_point() + geom_text(aes(label=ifelse(pSS>.2 | pSS<.07 | Nss>500 | N > 4e3, pitcher_name, ''))) + scale_color_gradientn(colors=c("blue", "black", "red")) )}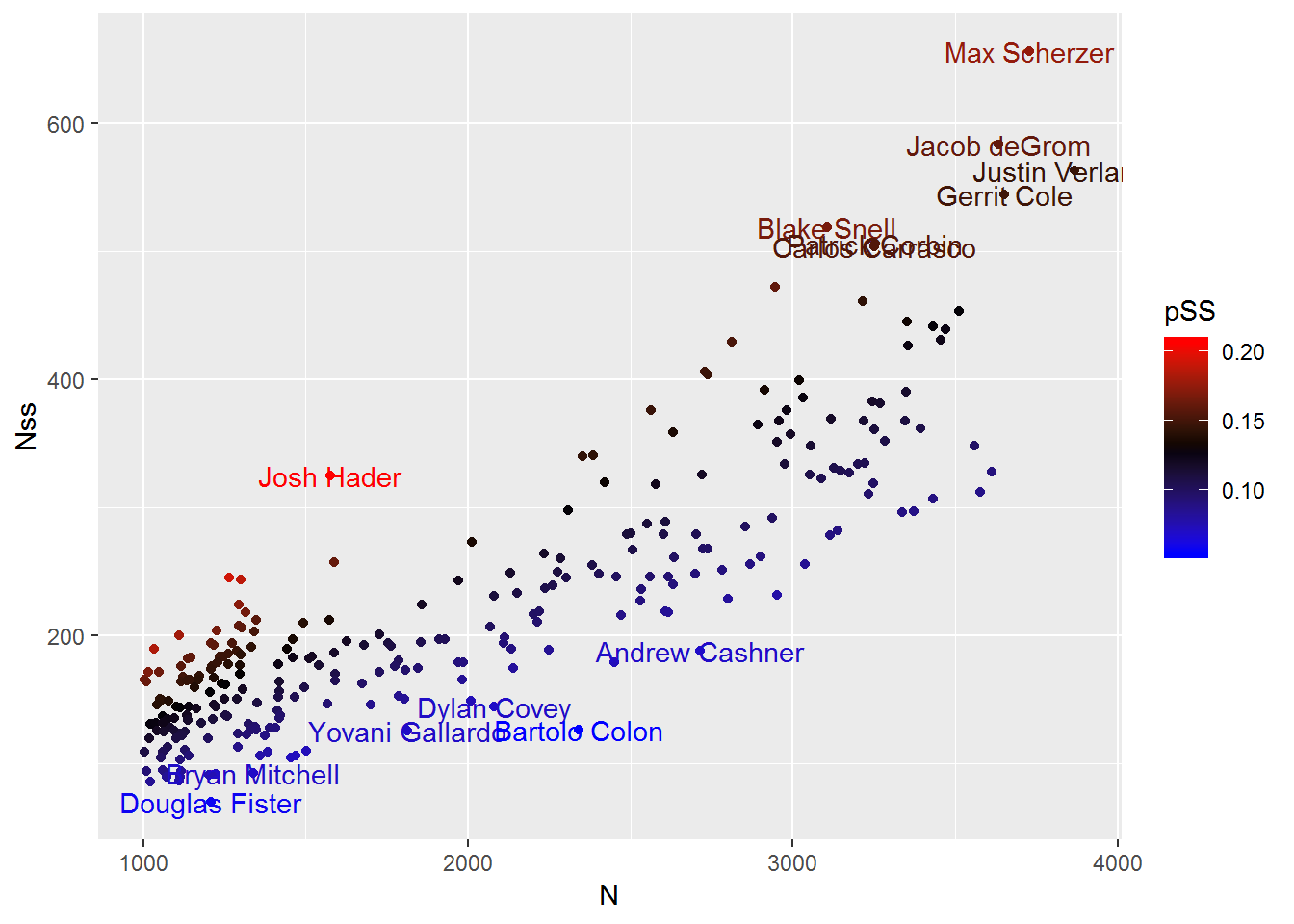

Where do swings and misses happen?

d2 %>% group_by(zone) %>% summarize(N=n(), Nss = sum(des %in% c("Swinging Strike", "Swinging Strike (Blocked)"))) %>% mutate(pSS = Nss / N) %>% arrange(desc(pSS))
## # A tibble: 14 x 4
##     zone      N   Nss    pSS
##    <dbl>  <int> <int>  <dbl>
##  1    NA  67971 15501 0.228 
##  2    14 160260 22099 0.138 
##  3     2  28565  3725 0.130 
##  4     3  24008  2990 0.125 
##  5    13 118329 14257 0.120 
##  6     1  25380  3010 0.119 
##  7     9  34948  4035 0.115 
##  8     8  36803  3801 0.103 
##  9     7  31026  3096 0.0998
## 10    12  75601  6656 0.0880
## 11     6  37556  3239 0.0862
## 12     5  41701  3367 0.0807
## 13    11  94465  7238 0.0766
## 14     4  36096  2658 0.0736

We have a lot of pitches with zone NA, so we’ll need to exclude these. I’m going to use the zones I created last time to plot these.

zone_values <- data.frame()
zones <- data.frame(
  zone = (c(rep(1:9, each=4), rep(11:14, each=6))),
  x = c(1,2,2,1,2,3,3,2,3,4,4,3,1,2,2,1,2,3,3,2,3,4,4,3,1,2,2,1,2,3,3,2,3,4,4,3,  0,1,1,2.5,2.5,0, 2.5,4,4,5,5,2.5, 2.5,5,5,4,4,2.5, 0,2.5,2.5,1,1,0),
  y = c(3,3,4,4,3,3,4,4,3,3,4,4,2,2,3,3,2,2,3,3,2,2,3,3,1,1,2,2,1,1,2,2,1,1,2,2,  2.5,2.5,4,4,5,5, 4,4,2.5,2.5,5,5, 0,0,2.5,2.5,1,1, 0,0,1,1,2.5,2.5)
)
zones$bs <- ifelse(as.numeric(zones$zone) <=9, "S","B")
ggplot() + geom_polygon(aes(x=x,y=y,fill=as.factor(bs), group=zone), zones, alpha=.5)

Now we can plot the swinging strike rates by zone.

SSdf <- d2 %>% group_by(zone) %>% summarize(N=n(), Nss = sum(des %in% c("Swinging Strike", "Swinging Strike (Blocked)"))) %>% mutate(pSS = Nss / N) %>% arrange(desc(pSS)) %>% filter(!is.na(zone)) %>% inner_join(zones)
## Joining, by = "zone"
ggplot(SSdf) + geom_polygon(aes(x=x,y=y,fill=pSS, group=zone), alpha=.8)  + scale_fill_gradientn(colours=c('blue','white','red'))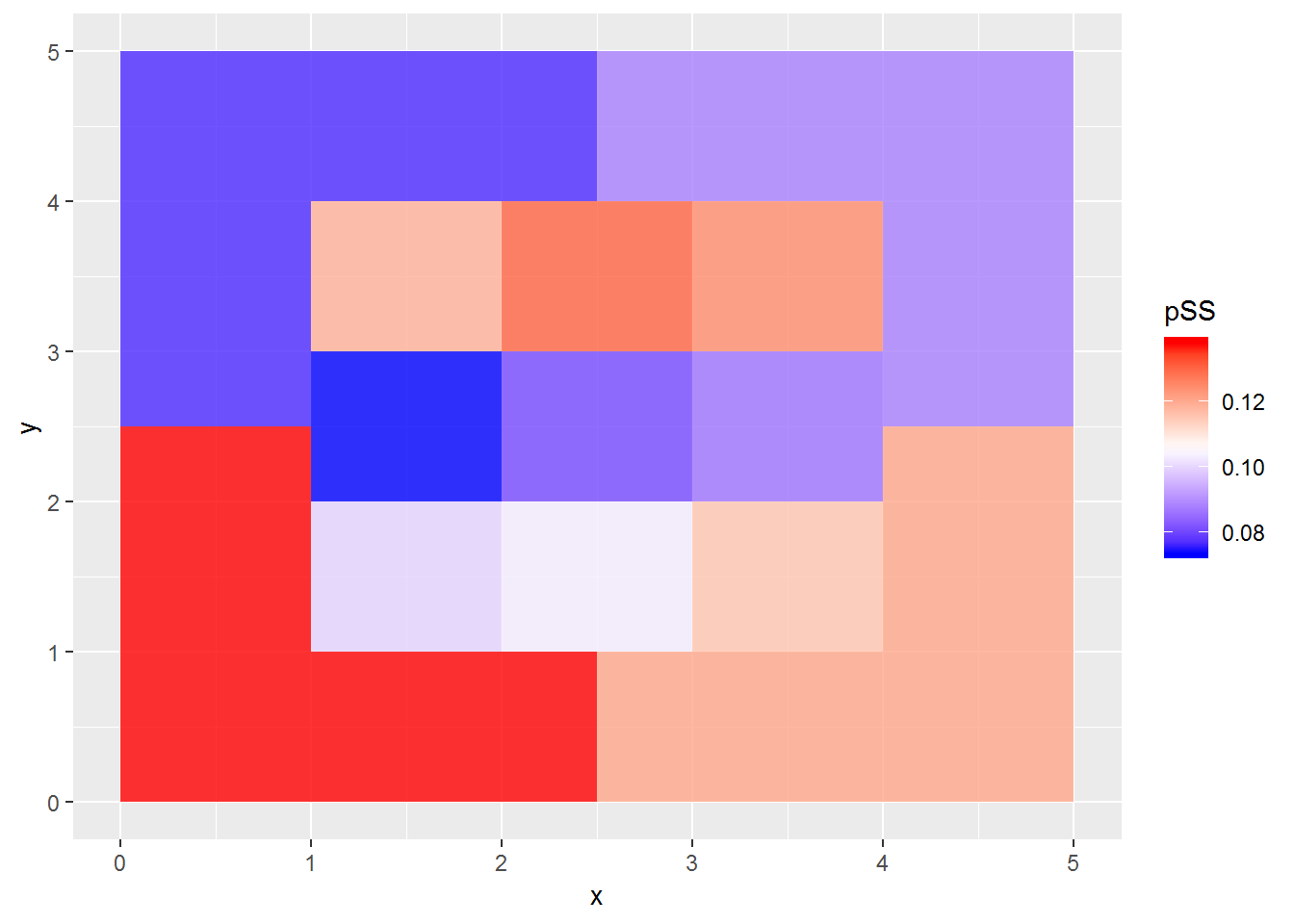

Again the results aren’t too surprising. Swings and misses occur most on low pitches outside the strike zone. If they were in the strike zone, they would be more likely to make contact. The lowest swinging strike rate is right in the center of the strike zone, which should be the easiest place to make contact.

So far we’ve been looking at the rate of swings and misses as a proportion of all pitches. What if we just look at pitches the batters swung at? We’ll have swings and misses on one hand, and contact on the other. In other words, given that the batter swung, what is the proportion that were misses?

SSdf2 <- d2 %>% group_by(zone) %>% summarize(N=n(), Ncontact=sum(des %in% c("Foul", "Foul (Runner Going)", "Foul Bunt", "Foul Tip", "In play, no out", "In play, out(s)", "In play, run(s)")), Nss = sum(des %in% c("Swinging Strike", "Swinging Strike (Blocked)"))) %>% mutate(pSSwung = Nss / (Nss + Ncontact)) %>% filter(!is.na(zone)) %>% inner_join(zones, by="zone")
ggplot(SSdf2) + geom_polygon(aes(x=x,y=y,fill=pSSwung, group=zone), alpha=.8)  + scale_fill_gradientn(colours=c('blue','white','red'))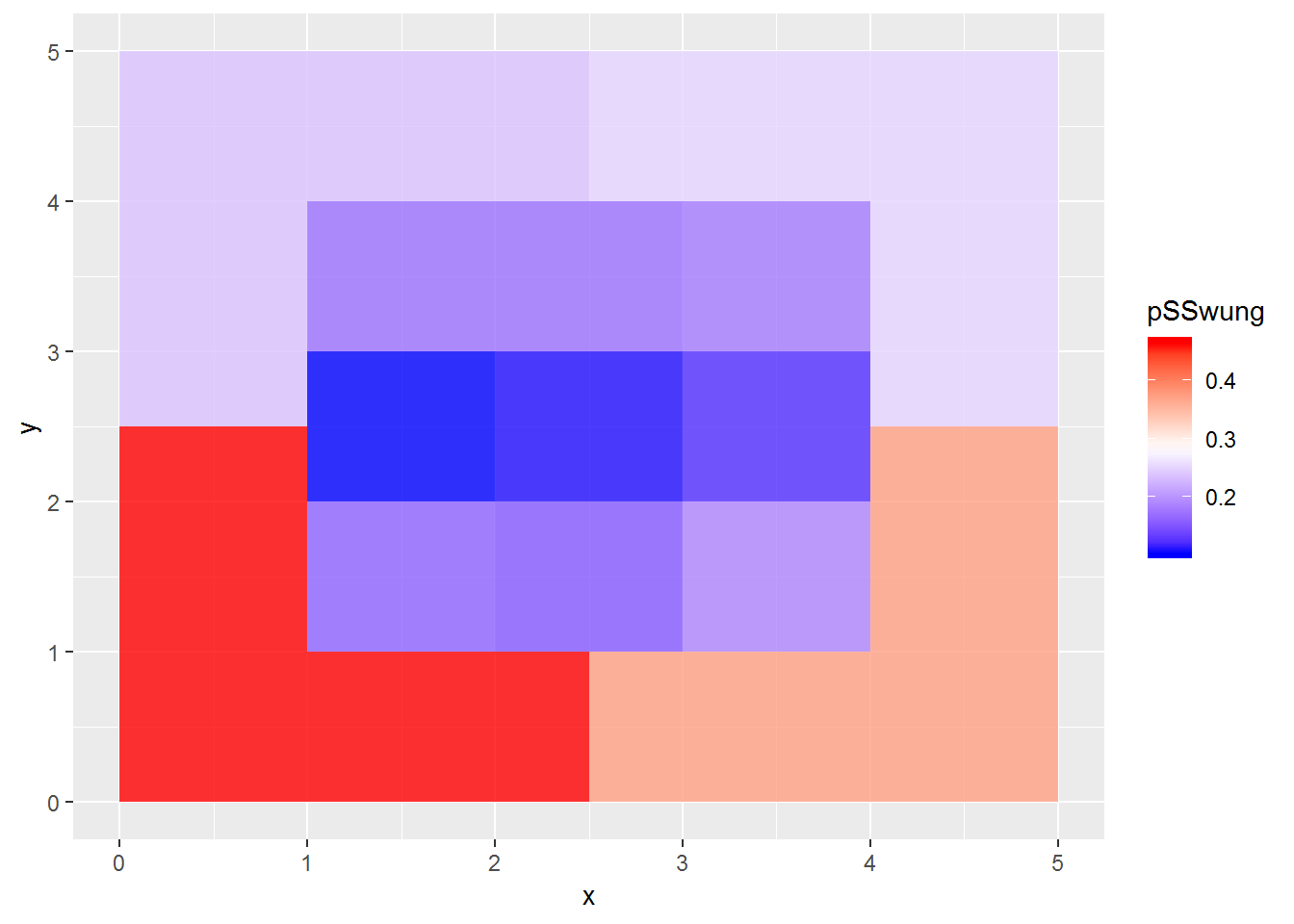

It’s highest below the strike zone, lowest in the center row of the strike zone. Similar trend as when looking at swinging strikes as a proportion of all pitches.